Logistic回归

回归是对一些数据点进行拟合，该拟合过程称为回归，这样的思想是用来做预测的。为什么能用来分类呢？假设有一个这样的函数，名称为Sigmoid
$$f(z) = {1 \over 1 + e^{-z}}$$

该函数显然随着z 增大$ f(z)$的值逼于1; 随着z的减小，$f(z)$等于 0。如果把自变量Z的值范围扩大到，如-20 到 20， f(z)就是一条突变的0到1的很陡曲线。

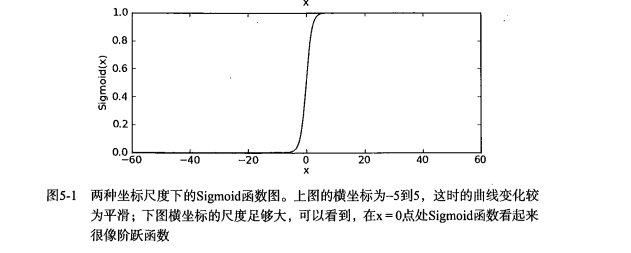
duck1

假设现在有如下数据集(含特征和类别)

特征1 x0    特征2 x1        类别
-0.017612	14.053064	     0
-1.395634	4.662541	     1
-0.752157	6.538620	     0
-1.322371	7.152853	     0
0.423363	11.054677	     0

假设 f(z) 的自变量 $z = w_0x_0 + w_1x_1$，将 z 代入 f(z)，该z使得f(z)产生突变，即可得到在0 < f(z) < 1

规定 f(z) < 0.5, 该数据归为第一类
规定 0.5 < f(z), 该数据归为第二类

所以求 $w_0$,$w_1$ 就是实现这一思想核心！

梯度

假设$z=f(x, y)$三维图像类似一座山峰的表面图形，像一顶帽子的图像。假设取山峰上一点$A(x_0, y_0, z_0)$，接下你想朝一个最陡峭的方向往上爬。该最陡峭的方向即为 A 点的梯度，所以梯度是个向量

梯度求法举例，假设有函数$z=f(x,y)$，梯度公式为

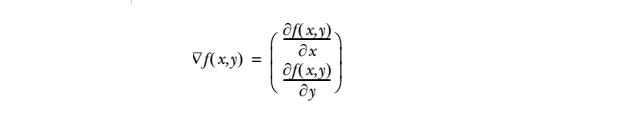
duck1

假设$z = 2x^2 + y^2$，则$\nabla f(x,y) = (4x, 2y)$，求在 $A(x_0, y_0, z_0)$的梯度为，将$x_0$， $y_0$ 带入梯度向量。A的梯度为 $(4x_0, 2y_0)$

还有另外一个移动步长k的概念，从A点沿着梯度方向$\nabla f(x,y)$(最陡峭方向) 爬一定的长度，就到了新的一个点A1,$A_1(x, y)=(x_0, y_0)+k(4x_0, 2y_0)$。再按照该方法就可以到新的点A2，这样一直爬下去A3, A4…..An就爬到了最高点An

梯度法得W

关于用梯度法求解系数w 的推导，请看这篇理解 logistic 回归。文中最后得出W和数据特征X，和类别Y(0或者1)的迭代关系式。

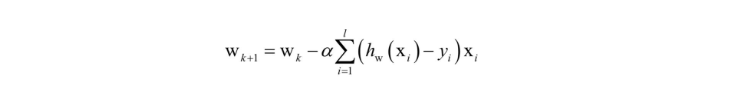
duck1

欢迎大家给我留言，提建议，指出错误，一起讨论学习技术的感受！